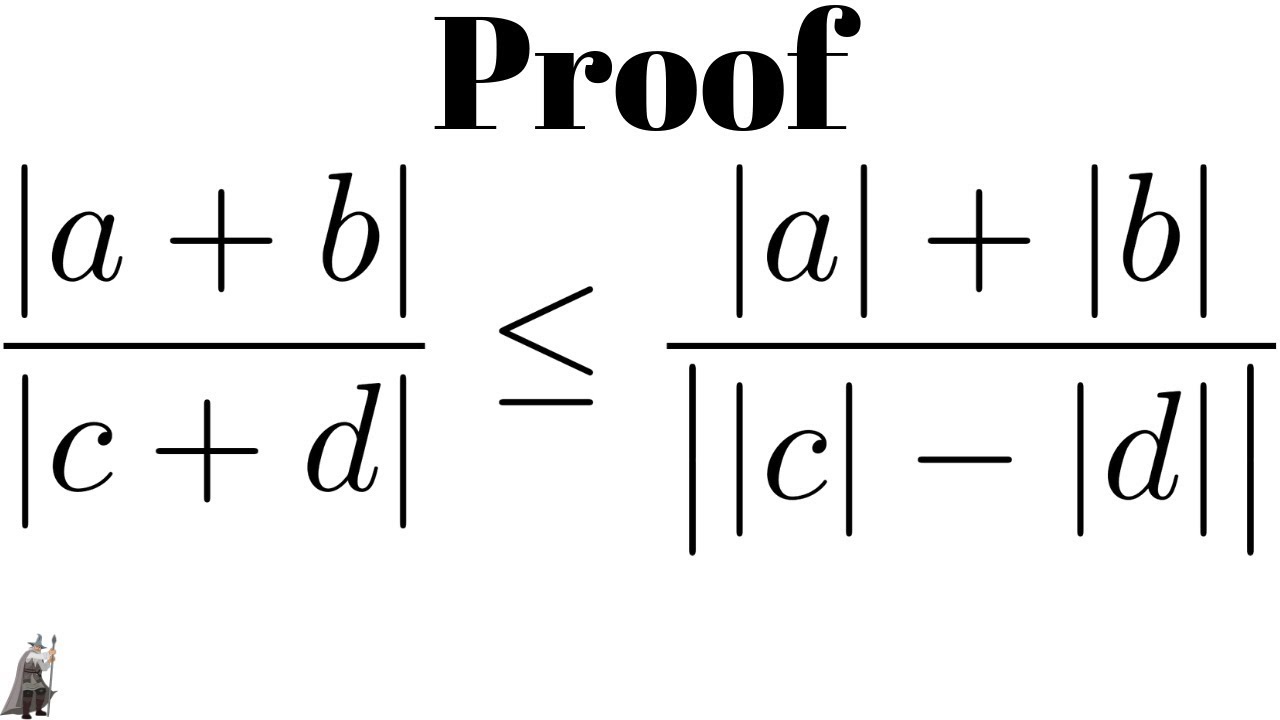
Inequality Proof using Both the Triangle Inequality and Reverse Triangle Inequality YouTube
The Cauchy-Schwarz Inequality holds for any inner Product, so the triangle inequality holds irrespective of how you define the norm of the vector to be, i.e., the way you define scalar product in that vector space.

Triangle Inequality TheoremDefinition & Examples Cuemath
The proof of the triangle inequality follows the same form as in that case. 8. Sas in 7. d(f;g) = max a x b jf(x) g(x)j: This is the continuous equivalent of the sup metric. The proof of the triangle inequality is virtually identical.

CALCULUS. Proof Triangle Inequality (5) YouTube
The triangle inequality theorem states that, in a triangle, the sum of lengths of any two sides is greater than the length of the third side. Suppose a, b and c are the lengths of the sides of a triangle, then, the sum of lengths of a and b is greater than the length c. Similarly, b + c > a, and a+ c > b.

proof of CauchySchwarz inequality, proof of Triangle Inequality Calculus Coaches
The triangle inequality is a theorem that states that in any triangle, the sum of two of the three sides of the triangle must be greater than the third side. For example, in the following diagram, we have the triangle ABC: The triangle inequality tells us that: The sum AB+BC must be greater than AC. Therefore, we have AB+BC>AC.
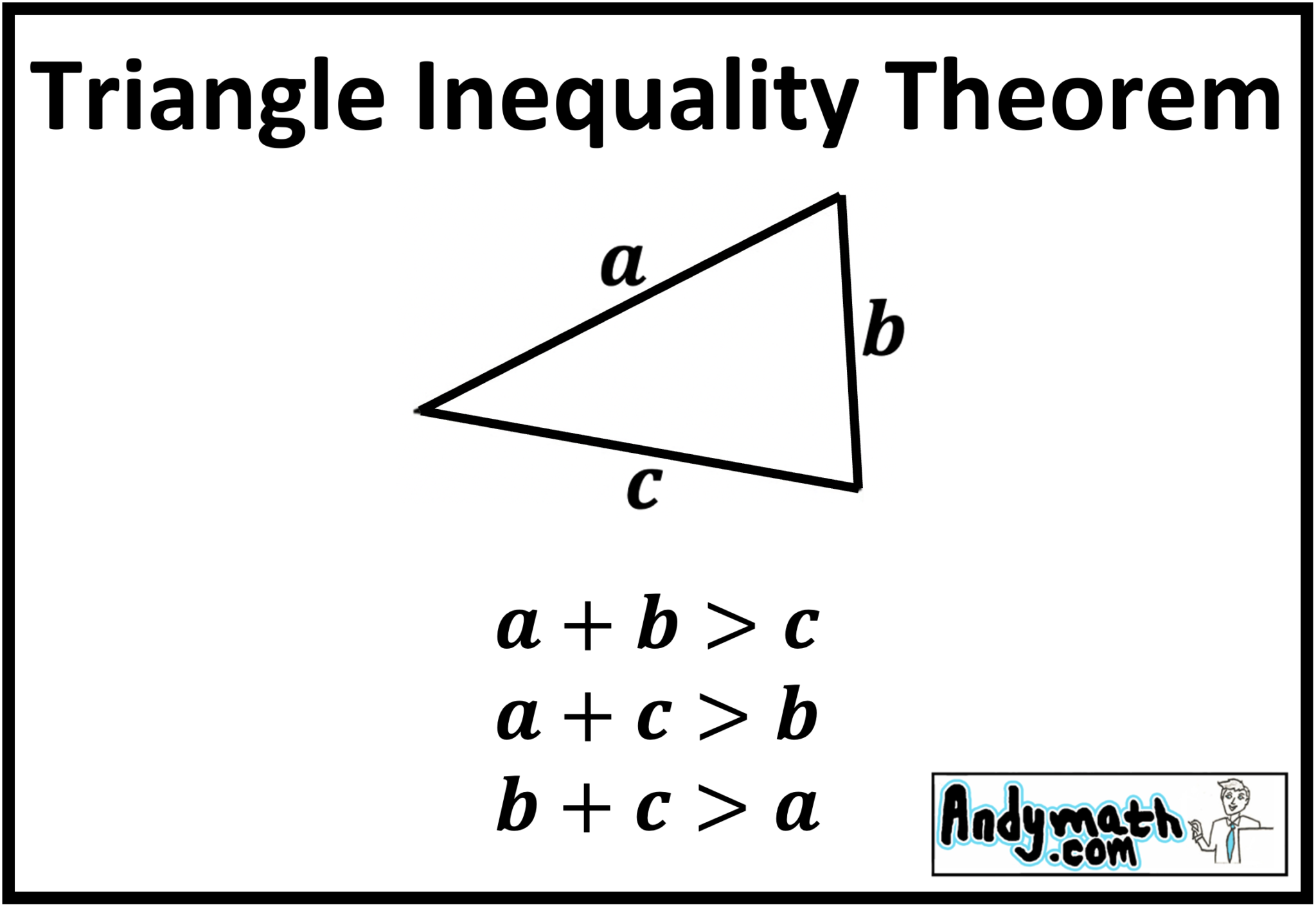
Triangle Inequality Theorem
Let us take our initial example. We could make a triangle with line segments having lengths 6, 8, and 10 units. This is because those line segments satisfy the triangle inequality theorem. 6 + 8 = 14 and 10 < 14. 8 + 10 = 18 and 6 < 18. 6 + 10 = 16 and 8 < 16.

Triangular inequality Proof (easy method) YouTube
The absolute value of a sum is less than or equal to the sum of the absolute values for any two real numbers. That is: |a+b| is less than or equal to |a|+|b|.

19+ triangle inequality theorem calculator Ikafnurhayati
Triangle Inequality. Let and be vectors. Then the triangle inequality is given by. (1) Equivalently, for complex numbers and , (2) Geometrically, the right-hand part of the triangle inequality states that the sum of the lengths of any two sides of a triangle is greater than the length of the remaining side. A generalization is.

Triangle Inequality Simple Proof YouTube
Use the Triangle Inequality Theorem. Check to make sure that the smaller two numbers add up to be greater than the largest number. 4 + 8 = 12 4 + 8 = 12 and 12 > 11 12 > 11 so yes these lengths make a triangle. Example 4.26.4 4.26. 4. Find the length of the third side of a triangle if the other two sides are 10 and 6.

Triangle Inequality Theorem Definition & Examples Cuemath
Proof of triangle inequality theorem Thus, we can conclude that the sum of two sides of a triangle is greater than the third side. Video Lesson on BPT and Similar Triangles 2,36,417 Also, read: Triangles Isosceles Triangle Theorems Congruence Of Triangles Class 9 Triangles For Class 10 Example Problems Q.1.

Reverse Triangle Inequality Proof YouTube
The proof is below. Proof Geometrically, the triangular inequality is an inequality expressing that the sum of the lengths of two sides of a triangle is longer than the length of the other side as shown in the figure below. The proof is as follows. Let a a and b b be real vectors.

Triangle Inequality for Real Numbers Proof YouTube
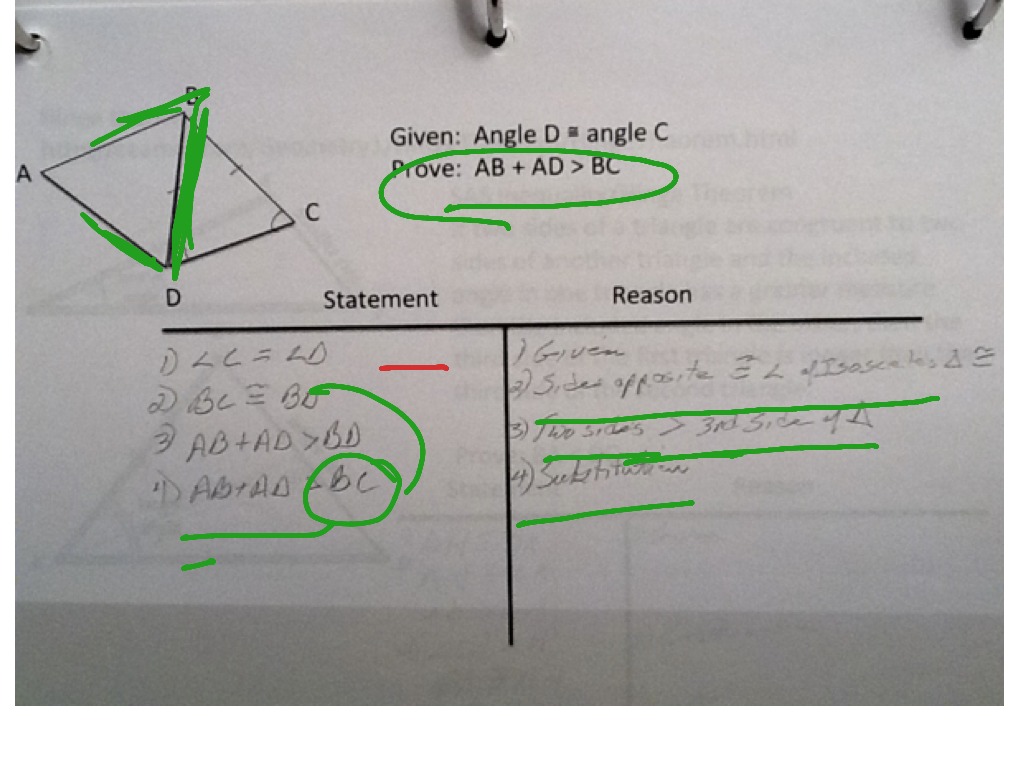
Proof: Extend BA to point D such that AD = AC, and join C to D, as shown below: We note that ∠ACD = ∠D, which means that in ∆ BCD, ∠BCD > ∠D. Sides opposite larger angles are larger, and thus: BD > BC AB + AD > BC AB + AC > BC (because AD = AC) This completes our proof. We can additionally conclude that in a triangle:

Proof Triangle Inequality Theorem Real Analysis YouTube
The triangle inequality is a very simple inequality that turns out to be extremely useful. It relates the absolute value of the sum of numbers to the absolute values of those numbers. So before we state it, we should formalise the absolute value function. 🔗 Definition 5.4.1. Let , x ∈ R, then the absolute value of x is denoted | x | and is given by

How to Prove the Triangle Inequality for Complex Numbers YouTube
The triangle inequality states that the sum of the lengths of any two sides of a triangle is greater than the length of the remaining side. It follows from the fact that a straight line is the shortest path between two points. The inequality is strict if the triangle is non- degenerate (meaning it has a non-zero area). Contents Examples Vectors
A guide on Triangle Inequality in every form of Mathematics
known that we can prove the triangle inequality in the broad sence, i.e. the ` '-version of (1.1), by algebraic argument. It is not exactly the triangle inequality in the sense of Euclidean geometry, because the point A is on the segment BC in case AB + AC = BC. For details of them, Subsection 1.2 (in particular Remark 1.3) will mention.
Sample proof of triangle inequality geometry ShowMe
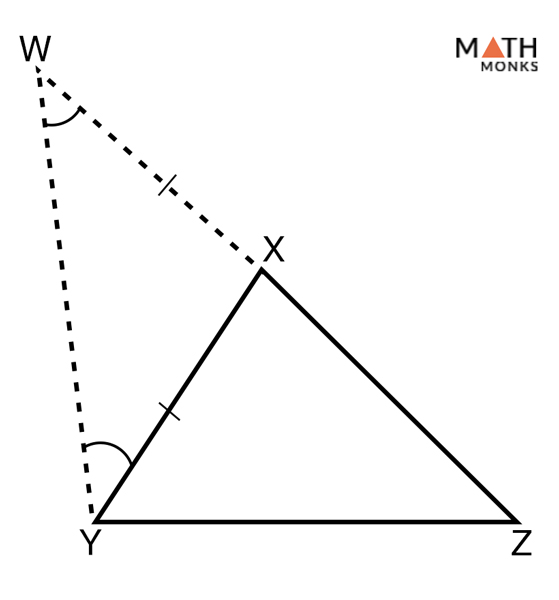
The proof of the triangle inequality uses the shortest distance property, which states that the shortest distance from a line L to a point P is a line perpendicular to L through the point P.
Triangle Inequality Theorem Definition, Proof, Examples
Triangle inequality theorem. The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side. Consider our 3−4−5 triangle example above. Add up any two sides of it. The sum of any of those two sides must be greater than the remaining side: 3+4>5 3 + 4 > 5.