
Calculus I Integrals of Exponential Functions YouTube
Exponential functions are those of the form \(f(x)=Ce^{x}\) for a constant \(C\), and the linear shifts, inverses, and quotients of such functions. Exponential functions occur frequently in physical sciences, so it can be very helpful to be able to integrate them. Nearly all of these integrals come down to two basic formulas:

CA.TF.5 Integrating Exponential Functions YouTube
Comments. The function $\mathop {\rm Ei}$ is usually called the exponential integral. Instead of by the series representation, for complex values of $ z $ ( $ x $ not positive real) the function $ \mathop {\rm Ei} ( z) $ can be defined by the integal (as for real $ x \neq 0 $); since the integrand is analytic, the integral is path-independent.

Question Video Finding the Integration of a Function Involving an Exponential Function Using
As mentioned at the beginning of this section, exponential functions are used in many real-life applications. The number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the derivative.Although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total growth.

Calculus I Integrals of Exponential Functions YouTube
The following is a list of integrals of exponential functions. For a complete list of integral functions, please see the list. Etisha Sharma, "Putting Forward Another Generalization Of The Class Of Exponential Integrals And Their Applications.," International Journal of Scientific Research in Mathematical and Statistical Sciences, Vol.10.

core pure 3 notes integrals involving exponentials
can be used, for example, the exponential integral EiHzL can be defined by the following formula (see the following sections for the corresponding series for the other integrals): EiHzL− 1 2 logHzL-log 1 z +â k=1 ¥zk kk! +ý. A quick look at the exponential integrals Here is a quick look at the graphics for the exponential integrals along.

PPT EXPONENTIAL FUNCTIONS DIFFERENTIATION AND INTEGRATION PowerPoint Presentation ID6646262
Learning Objectives. 2.7.1 Write the definition of the natural logarithm as an integral.; 2.7.2 Recognize the derivative of the natural logarithm.; 2.7.3 Integrate functions involving the natural logarithmic function.; 2.7.4 Define the number e e through an integral.; 2.7.5 Recognize the derivative and integral of the exponential function.; 2.7.6 Prove properties of logarithms and exponential.

Exponential Function Formula of Integration YouTube
The exponential function has a base of e, so we use the integral formula, ∫ e x x d x = e x + C. Since the exponent has − 1 before x, we'll need to use the substitution method to integrate the expression. u = − x d u = − 1 ⋅ d x − d u = d x. Rewrite ∫ e − x x d x in terms of u and d u.

PPT 5.4 Exponential Functions Differentiation and Integration PowerPoint Presentation ID
Well, to find the antiderivative (integral) of an exponential function, we will apply the same three steps, except instead of multiply, we will divide! Rewrite. Divide by the natural log of the base. Divide by the derivative of the exponent. ∫ a b x d x = a b x b ( ln a) + C. a: The base of the exponential function.
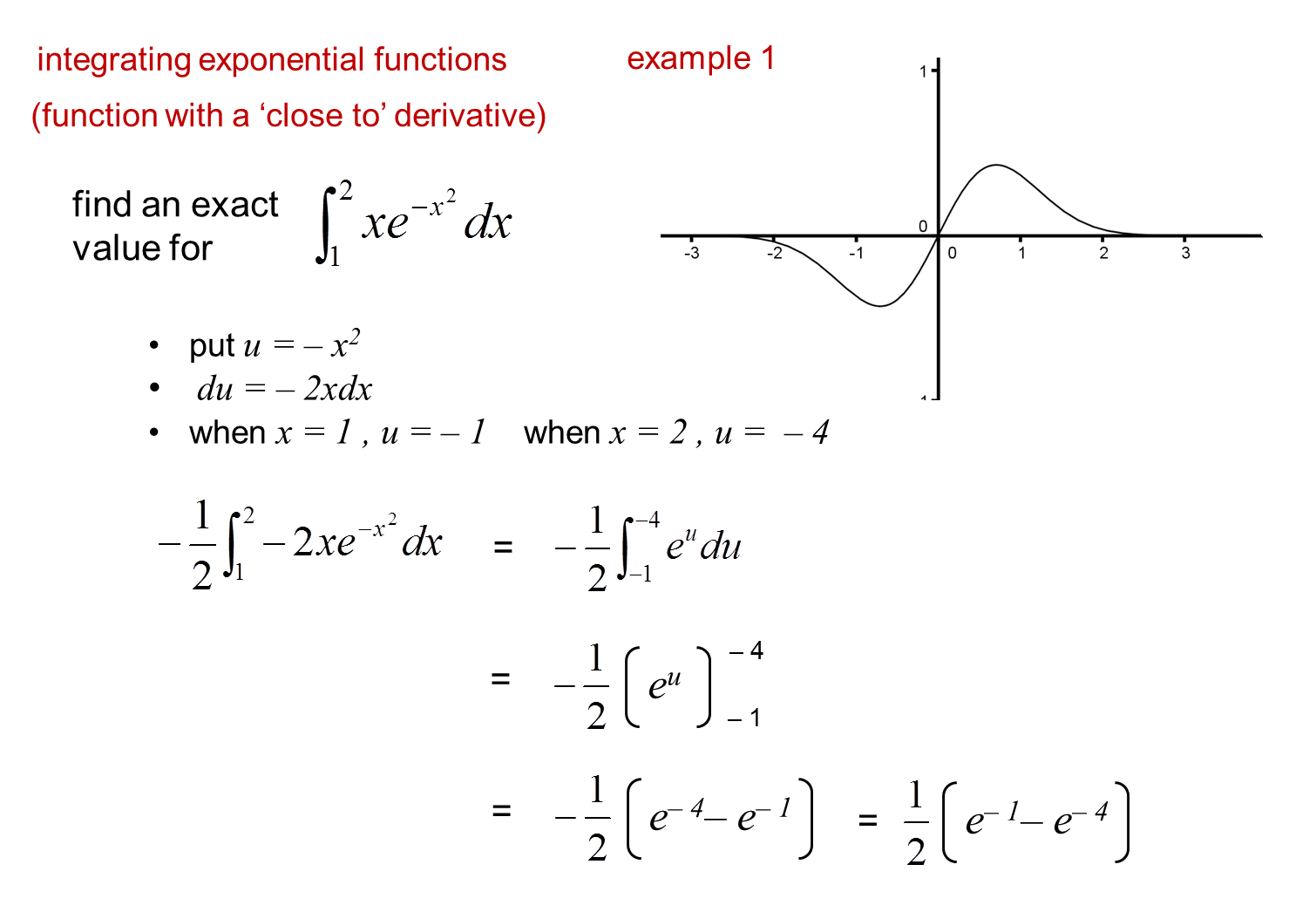
core pure 3 notes integrals involving exponentials
Finding the derivative of an exponential function is pretty straightforward since its derivative is the exponential function itself, so we might be tempted to assume that finding the integrals of exponential functions is not a big deal. This is not the case at all. Differentiation is a straightforward operation, while integration is not.

Calculus Integration of Exponential Functions
The following problems involve the integration of exponential functions. We will assume knowledge of the following well-known differentiation formulas : , and. is any positive constant not equal to 1 and is the natural (base ) logarithm of . These formulas lead immediately to the following indefinite integrals :
Integral of Exponential Functions Basic Integration Formulas YouTube
Let's rectify that here by defining the function f(x) = ax in terms of the exponential function ex. We then examine logarithms with bases other than e as inverse functions of exponential functions. Definition: Exponential Function. For any a > 0, and for any real number x, define y = ax as follows: y = ax = exlna.

How to integrate exponential functions ExamSolutions Maths Revision Tutorials YouTube
Exponential Integral. where the retention of the notation is a historical artifact. Then is given by the integral. This function is implemented in the Wolfram Language as ExpIntegralEi [ x ]. The exponential integral is closely related to the incomplete gamma function by.

core pure 3 notes integrals involving exponentials
Since the derivative of e^x is itself, the integral is simply e^x+c. The integral of other exponential functions can be found similarly by knowing the properties of the derivative of e^x.
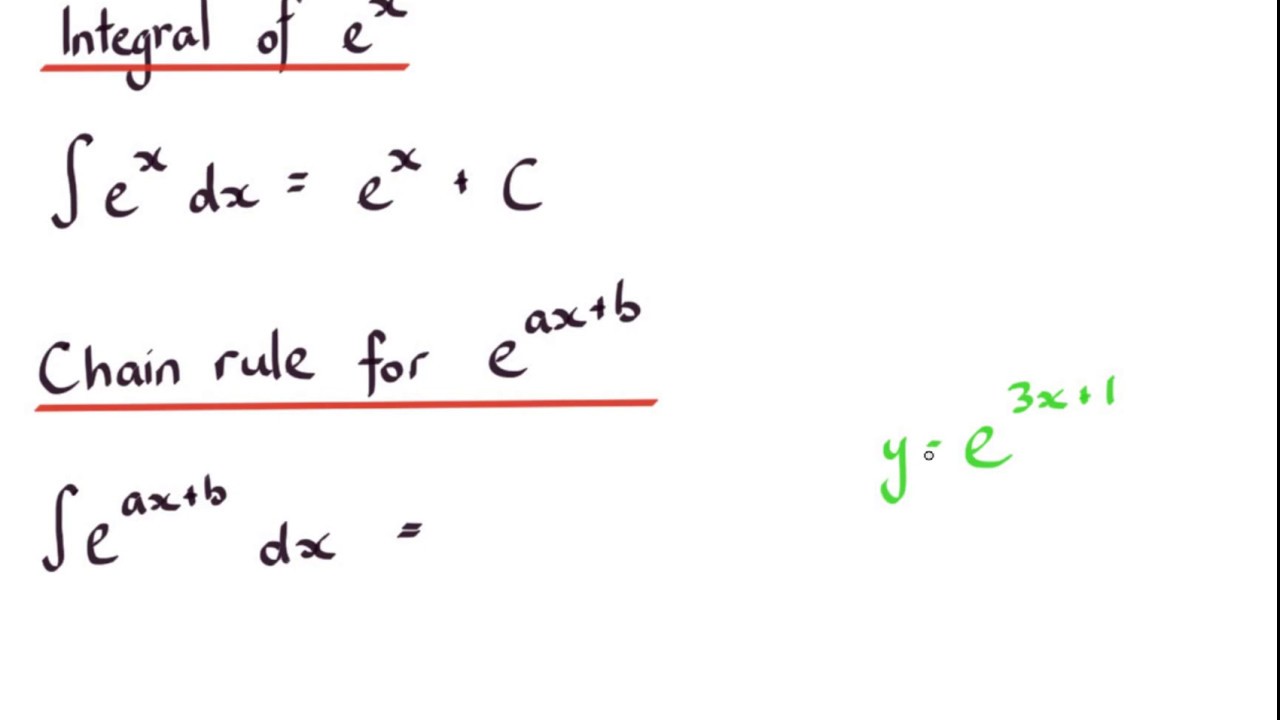
Integration Part 6 Exponential functions YouTube
5.6.2 Integrate functions involving logarithmic functions. Exponential and logarithmic functions are used to model population growth, cell growth, and financial growth, as well as depreciation, radioactive decay, and resource consumption, to name only a few applications. In this section, we explore integration involving exponential and.

Integration Exponential Functions YouTube
The Derivative of the Exponential. We will use the derivative of the inverse theorem to find the derivative of the exponential. The derivative of the inverse theorem says that if f f and g g are inverses, then. g′(x) = 1 f′(g(x)). g ′ ( x) = 1 f ′ ( g ( x)). Let. f(x) = ln(x) f ( x) = ln ( x) then. f′(x) = 1 x f ′ ( x) = 1 x.

Integrating Exponential Functions Examples 3 and 4 YouTube
The exponential integrals , , , , , , and are defined for all complex values of the parameter and the variable . The function is an analytical functions of and over the whole complex ‐ and ‐planes excluding the branch cut on the ‐plane. For fixed , the exponential integral is an entire function of .